Hinweis: Für Formeln verwende ich auf dieser Seite MathML, was leider noch nicht von allen Browsern unterstützt wird.
Eine wichtige Erkenntnis ist, dass Teleskope uns kein 1:1 Abbild der Wirklichkeit zeigen. Dies ist sehr leicht zu veranschaulichen, indem ein heller Stern – in großer Höhe und bei gutem Seeing – im Bereich der Übervergrößerung () betrachtet wird.
Beispiel: Capella
Nehmen wir den Stern Capella als Testfall – eigentlich ein Mehrfachsystem, wobei die Hauptkomponente den 12-fachen Durchmesser der Sonne hat. Die Entfernung beträgt 43 Lichtjahre und es ergibt sich aus unserer Perspektive ein scheinbarer Winkeldurchmesser von ca. 0,00015" für den größten der vier bekannten Sterne. Mit einem 200-mm-Teleskop liegt die Vergrößerung dann im Bereich von 400-fach. Somit würde Capella im Okular als ein winziges Scheibchen erscheinen.Die Dichte der Lichtrezeptoren auf unserer Netzhaut erlaubt bestenfalls noch Objekte mit Winkeldistanzen im Bereich von 1' zu trennen. Ein schöner Test für die Augen ist der Mehrfachstern ε Lyr, dessen Hauptkomponenten rund 3,5' voneinander entfernt stehen – einfach mal ausprobieren!
Das Ergebnis dieser Abschätzung bedeutet, dass uns Capella auch bei Maximalvergrößerung als perfekter Punkt erscheinen sollte.
Beugungsbild eines Sterns
Die Realität sieht jedoch anders aus: Capella ist bei hoher Vergrößerung (und gutem Seeing) ein kleines Scheibchen, umgeben von Ringen, die nach außen hin schwächer werden. So sieht Capella natürlich nicht wirklich aus, sondern wir sehen eigentlich nur das vom Teleskop erzeugte Beugungsbild. Es erinnert an Spaltexperimente mit Laser-Licht im Physikunterricht. Der Spalt, der hier die Beugung verursacht, ist die runde Teleskopöffnung.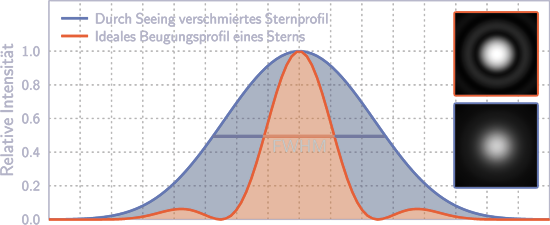
Dabei bezeichnet man die innerste Zone, das Beugungsscheibchen, auch als Airy-Disk.
Das Rayleigh-Kriterium
Das Auflösungsvermögen eines Teleskops wird grundsätzlich durch seine beugende Eigenschaft bestimmt. Je näher zwei Sterne beieinander stehen, desto stärker überlagern sich deren Beugungsbilder, bis sie schließlich zu einem Objekt verschmelzen. Lord Rayleigh formulierte zur Trennung zweier Sterne ein im Grunde willkürliches Kriterium:
Zwei Sterne gelten als eben noch getrennt, wenn der erste dunkle Ring des
einen Sterns durch den Mittelpunkt des Airy-Scheibchens des anderen verläuft.
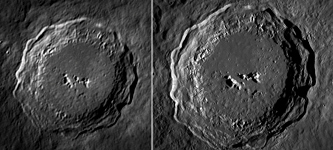
Die sieht in der Praxis wie folgt aus.
Links ist das beugungsbild eines Einzelsterns zu sehen.
Das rechte Sternpaar ist deutlich getrennt und somit voll aufgelöst.
In der Mitte ist der Grenzfall für das Rayleigh-Kriterium zu sehen.
Hier ist noch offensichtlich, dass es sich nicht um einen Einzelstern handelt.
einen Sterns durch den Mittelpunkt des Airy-Scheibchens des anderen verläuft.

Die Formel für den Winkel , unter dem zwei Sterne gerade noch als zwei Objekte wahrgenommen werden, lautet: Dieser Winkel wird i.A. als das Auflösungsvermögen eines Teleskops angegeben. Dabei ist der Öffnungsdurchmesser des Teleskops und die Wellenlänge des Lichts. Es ist bei Anwendung der Formel darauf zu achten, dass und in der gleichen Einheit eingesetzt werden. Das Ergebnis hat dann die Einheit Grad ().
Beispielrechnungen
Mit der obigen Formel lassen sich einige Fälle durchspielen. Das folgende Diagramme zeigt das Auflösungsvermögen nach Rayleigh in Abhängigkeit der Wellenlänge und für fünf ausgewählte Öffnungsdurchmesser.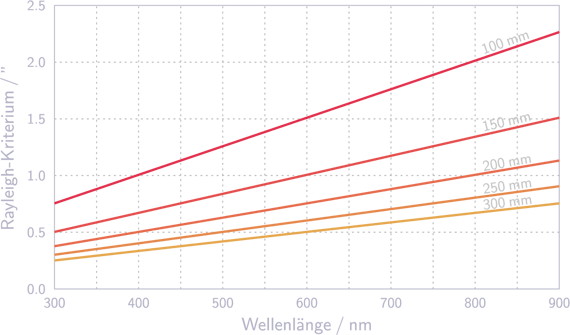
Für ein 200-mm-Teleskop und für typische Filterbereich in Zahlen ausgedrückt:
| Bereich | NUV | Blau | Grün | Rot | NIR |
|---|---|---|---|---|---|
| Wellenlänge (ca.) | 350 nm | 450 nm | 550 nm | 650 nm | 800 nm |
| Rayleigh | 0,44″ | 0,57″ | 0,69″ | 0,82″ | 1,0″ |
Oft wird bei der Planeten- und Mondfotografie unter schwierigen Seeing-Bedingungen zu einem IR-Passfilter gegriffen. Dieser "beruhigt" das Seeing und verbessert so die Ergebnisse. Anhand der Tabelle ist jedoch klar, dass dies ein Kompromiss unter Inkaufnahme einer schlechteren Auflösung ist.
Auflösung verbessern / optimieren
Möchte man eine möglich gute Auflösung erzielen, bieten sich offenbar zwei Strategien an – Die Anforderungen an das Seeing steigen dabei natürlich:- Öffnungsdurchmesser: Eine gute Qualität der optischen Elemente vorausgesetzt, erzielt man mit einem größeren Teleskop eine bessere Auflösung.
- Wellenlänge: Aus einem vorhandenen Teleskop lässt sich fotografisch unter Umständen mehr herausholen, indem im blauen oder sogar im nahen UV aufgenommen wird:
- Das Teleskop muss in diesem Bereich gut korrigiert sein. Achromaten fallen hier i.A. raus.
- Ein UV-Passfilter ist vorhanden (z.B. Johnson-U oder Venusfilter).
- Filter-Alternativen: Violettfilter Wratten #47, Blaufilter.
- Nicht bei allen Motiven sinnvoll. Bietet sich für Sonne und Mond an.
[12.02.2018]